查詢時請注意選擇相應的產品編號
| Enge-l?BrewerP和auling金屬的價鍵理論 | |||
|---|---|---|---|
|
Pauling在上世紀30年代提出了解釋金屬結合力的一種觀點。金屬結合起源于相鄰原子間價電子所形成的共價鍵,可以把這種鍵看成是未飽和的共價鍵,因為金屬一般價電子少,配位數高,由于電子不夠全面供應,金屬原子不足以在所有相鄰原子間形成共價鍵,只有輪流和周圍的原子形成單電子結合和雙電子結合的共價鍵,所以可認為是未飽和的共價鍵。Pauling認為這種鍵是無序分布,每一個原子平均只參與一個結合鍵,而電子在這些鍵中共振,使能量降低,晶體的穩定性提高。所以,金屬被認為是金屬的不同原子之間形成一個電子和兩個電子共價結合的各種結構,而金屬鍵就是在這些所有不同結構之間的電子共振。
Pauling從化學的觀點系統研究了金屬的價與鍵的問題,認為金屬價(即金屬參與鍵合的未配對電子數)與金屬的熔點、沸點、硬度等性能有關。應用金屬本身的一些性質,至少可以近似地指出金屬的價數。從鉀開始的元素周期中,如果假定鉀的金屬價為1,鈣的金屬價為2,那么可以看到在價數與性質之間存在著一種預期的聯系。金屬鈣比金屬鉀有更高的硬度、強度與密度,它的熔點、沸點、溶化熱函與蒸發熱函也比鉀高些,一般說來,它們的這些性質恰好與這樣的假定相符。Pauling根據元素的金屬價和金屬中原子間距和實驗數據以及經驗公式(4),推出一套相當完整的金屬半徑。D(n)=D(l)-01600log(n)式中D(n)為鍵距,D(l)為單鍵鍵距,即n=1的D(n)值,n為鍵數,即共價鍵上的共價電子對數,等于金屬的價除以配位數。隨著金屬共振價鍵理論的發展,
Pauling采用更加可靠的方法,通過對鍵數和共振能的校正,從實驗的原子間距重新修訂計算出了金屬的價和金屬半徑,如表1所示。它所用經驗公式為式,式中v的共振結構數。D(n)=D(l)-01770log{n[1+01064(v-1)]}總之,公式(4)與(5)是確定金屬價與晶體結構信息鍵長關系的經驗公式,正如Pauling所述,經驗公式應該是不很準確的。然而,從公式得出得有關電子構型、鍵數、金屬和金屬間化合物的價等結論,還是比較可靠的。2.Enge-lBrewer金屬價鍵理論
Engel和Brewer修正和發展了Pauling的金屬價鍵理論,不僅把金屬原子的價電子結構與金屬及其合金的鍵合能關聯起來,而且把原子的價電子結構與金的晶體結構關聯起來。其理論可歸納為兩條規則。
(金屬或合金的鍵合能取決于每個原子能夠鍵合的未成對電子的平均數。如果由于增加電子所放出的鍵合能夠補償所需的激發能,則具有較多未成對電子的激發電子組態比基態電子組態更為重要。如圖3所示,該圖稱為Born-Hober循環,。
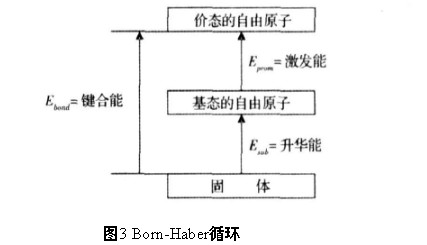
其中能量關系式如式)所示,式中Esub是升華能,Ebond是鍵合能,Eprom是激發能。Esub=Ebond-Eprom(6)(2)金屬的晶體結構取決于鍵合中每一原子的s和p軌函的平均數,也就是取決于其/準備好鍵合0態中原子的未成對的s和p電子平均數。當鍵合中s和p電子數之和少于或等于115時,出現體心立方晶體結構(bcc)。當鍵合中s和p電子數之和在117~211之間時,出現六方密堆晶體結構(hcp)。當鍵合中s和p電子數之和在215~310的范圍時。出現立方密堆晶體結構(ccp)。當鍵合中s和p電子數之和接近于4時,出現的是非金屬的金剛石結構。根據金屬升華能的實驗值和不同價態能級相對基態能級激發能的實驗值,結合公式(6),Brewer確定了金屬的價電子組態。
|
| 上一篇:鍵參數表征化學鍵性質的某些物理量 | 下一篇:Hume-Rothery電子濃度理論 |
|---|
無法在這個位置找到: xy/left.htm
